Nonintegrable Constraints in Mechanics

Over the summer of 2022, I led a math undergraduate research program at Cornell University on the subject of nonintegrable constraints in mechanics. Their research project was on studying the long-term behavior of mechanical systems subjected to nonholonomic and impact constraints.
Below are some of their resources and a small summary of their work is to the right.
- Primer on symplectic geometry.
- Primer on invariants in dynamical systems.
- Worksheet on geometric mechanics.
- Worksheet on nonholonomic systems.
- Worksheet on hybrid and impact systems.
Chaplygin sleigh with impacts

L.P.O. Reduction
Given a left-invariant Hamiltonian ![]() , Lie-Poisson reduction allows for the (continuous) dymanics to be reduced to
, Lie-Poisson reduction allows for the (continuous) dymanics to be reduced to ![]() with the dynamics
with the dynamics
![]()
If an impact occurs at a set ![]() and
and ![]() is a right coset, the impact system can be reduced to
is a right coset, the impact system can be reduced to ![]() with dynamics
with dynamics
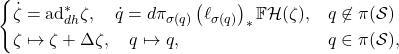
where ![]() such that
such that ![]() and
and ![]() is a section.
is a section.
Hybrid transfer operator
Let ![]() be a hybrid system with associated flow
be a hybrid system with associated flow ![]() . The transfer operator is an induced flow on
. The transfer operator is an induced flow on ![]() given by
given by
![]()
The long-time properties of this operator encode statistical information about the orbits of the system (e.g. ergodic properties).

Left: An animation of the values of ![]() for the bouncing ball subject to dissipation where
for the bouncing ball subject to dissipation where ![]() is a Gaussian distribution.
is a Gaussian distribution.
Right: All trajectories in this system are Zeno. As time progresses, this image displays the initial conditions that “disappear.”