Nonholonomic mechanics

systems subject to nonintegrable constraints

For a given configuration space, $Q$ , and a Lagrangian function $L:TQ\to\mathbb{R}$ , the principle of least action states that the physical motion of the system is a critical path of the action functional

$\begin{equation*} \mathcal{A}[\gamma] = \int \, L(\dot{\gamma})\, dt, \end{equation*}$

which produces the famous Euler-Lagrange equations

$\begin{equation*} \delta\mathcal{A} = 0 \implies \frac{d}{dt}\frac{\partial L}{\partial\dot{\gamma}} - \frac{\partial L}{\partial\gamma} = 0. \end{equation*}$

If the system is subjected to (nonintegrable) velocity constraints, the principle of least action is no longer valid. In the case of linear constraints, this manifests as specifying a linear subbundle $\mathcal{D}\subset TQ$ and the equations of motion are prescribed via

$\begin{equation*} \left( \frac{d}{dt} \frac{\partial L}{\partial\dot{\gamma}} - \frac{\partial L}{\partial\gamma} \right) \delta\gamma = 0, \quad \delta\gamma\in\mathcal{D}. \end{equation*}$

These systems can exhibit wonderfully paradoxical behavior; e.g. energy and volume need not be conserved.

Hybrid dynamics

Systems that are both continuous and Discrete

Hybrid dynamical systems are systems that exhibit both continuous and discrete time evolution. The dynamics can be described by

$\begin{equation*} \begin{cases} \dot{x} = f(x), & x\not\in \mathcal{S}, \\ x^+ = \Delta(x), & x\in \mathcal{S}. \end{cases} \end{equation*}$

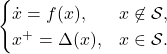
A distinguished class of hybrid systems are those modeling legged locomotion; the continuous dynamics describe the swing phase while the discrete dynamics describe the touchdown and liftoff events (switching which leg is in contact with the ground). Consequently, the location and stability of periodic orbits is fundamental as they represent stable walking gaits.

One phenomenon that is particularly vexing is Zeno; a trajectory is Zeno if it undergoes infinitely many discrete transitions in a finite amount of time. This is ubiquitous in inelastic impact systems and almost never occurs in elastic systems.

Robotic perception

using geometry to align data

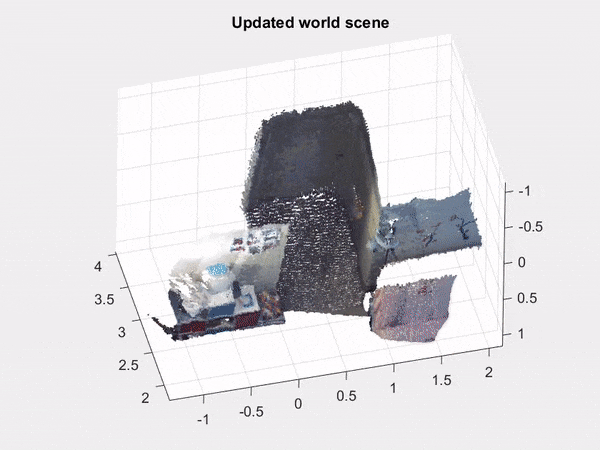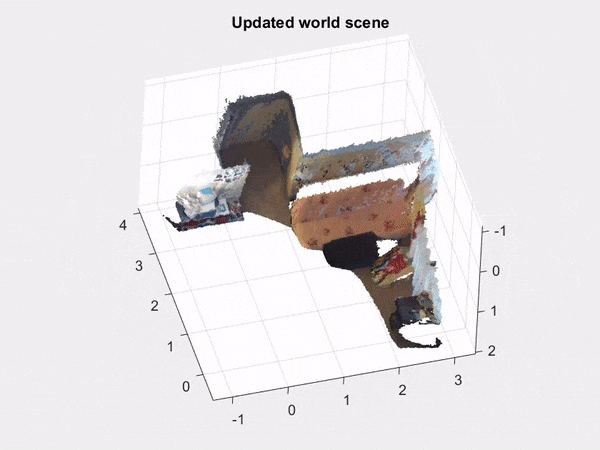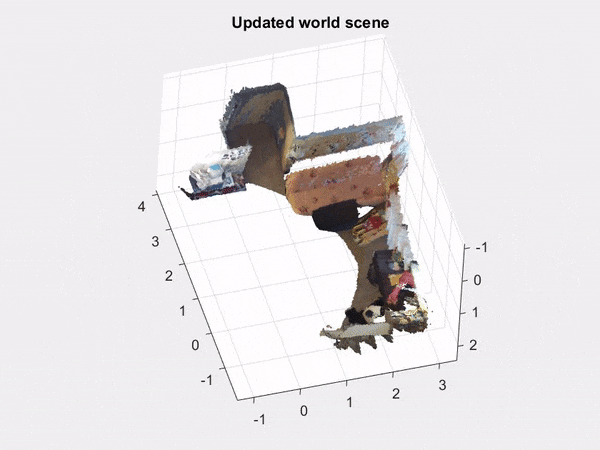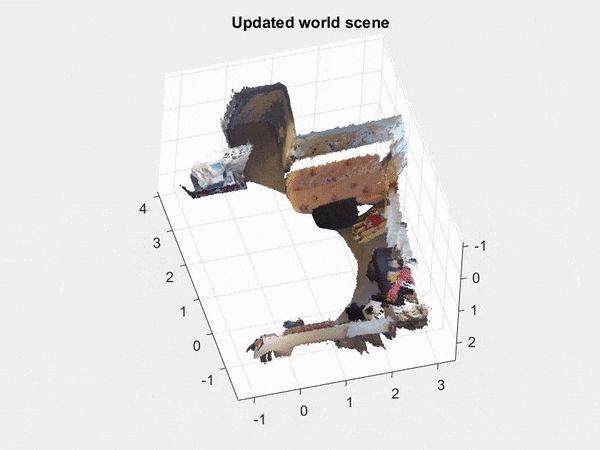
The problem of sensor registration is defined as finding the transformation between two sensors with overlapping measurement. A concrete example of this is pose estimation of a mobile robot; the transformation between two successive pictures of the environment is related to the change in the pose of the robot.

In collaboration with CURLY at the University of Michigan, we developed a novel mathematical framework that represents the discrete data of a point cloud as a continuous function in a reproducing kernel Hilbert space. This paradigm has the distinct advantage of being independent of the signal resolution and offers a closed-form derivation of the Riemannian gradient and Hessian to allow the use of gradient descent to calculate the pose.

Teaching slides from NA 568.